Textos de acceso libre
Cartas robadas a una princesa checa
Dr. Pablo Amster *
El libro La matemática como una de las bellas artes comienza con una historia extraída de una serie checa de dibujos animados. Se trata de una princesa cuya mano es disputada entre muchos pretendientes que intentan seducirla, ya sea ofreciéndole obsequios o haciendo gala de deslumbrantes destrezas. Uno a uno van pasando los candidatos y, uno a uno, van fracasando; más aun, el rostro de la princesa no deja traslucir ni siquiera la más mínima emoción. La serie se cierra con un último galán que humildemente le ofrece unos anteojos y con ello logra, por fin, conquistarla. El fracaso de los otros pretendientes le hizo comprender que la princesa no se conmovía ante las maravillas ofrecidas por una razón muy simple: no era capaz de verlas.
La historia ha sido usada para hablar de la belleza matemática; más precisamente, para dar cuenta de un problema: ¿cómo hacer para transmitir esa belleza a quien nunca la ha experimentado? La matemática es capaz de brindar un gran placer estético, pero sólo cuando uno se encuentra suficientemente preparado para ello; por eso, antes de hablar de nuestras "bellezas" conviene adoptar la actitud del galán humilde y ofrecer los elementos básicos que permitan apreciarlas. En el libro mencionado se ofrece una justificación de este proceder, algo entusiasta:
"… hablar de Matemática no es solamente demostrar el teorema de Pitágoras: es, además, hablar del Amor y contar historias de princesas. También en la Matemática hay belleza; como dijo el poeta Fernando Pessoa, El binomio de Newton es tan hermoso como la Venus de Milo; lo que pasa es que muy poca gente se da cuenta."[1]
En estas notas veremos una descripción elemental de un sistema formal que aparece en un conocido escrito, cuyo tema principal está basado justamente en lo que se ve y lo que deja de verse: nos referimos a "El seminario sobre La carta robada", del psicoanalista francés Jacques Lacan.[2]
El comienzo es muy sencillo: se trata de formar todas las secuencias posibles mediante un alfabeto compuesto por dos signos. Lacan emplea los signos + y –, y los piensa como transcripciones de las tiradas de una moneda: si sale cara anotamos un +, y un – en caso de que salga ceca. En definitiva, dice, en eso consiste el discurso: una concatenación azarosa de significantes. Cualquier combinación, hasta la más caprichosa, es verosímil: el azar de la moneda le da el derecho de producir cualquier secuencia.
La cuestión empieza verdaderamente cuando se opera una transcripción a un nuevo alfabeto, esta vez constituido por los números 1, 2 y 3. La forma de pasar de un sistema al otro recuerda vagamente a las secuencias de ADN, en donde las "palabras" formadas por tres letras que pueden ser A, T, C o G se traducen para formar las cadenas de aminoácidos de la proteína. Sólo que en nuestro caso el alfabeto original tiene únicamente dos símbolos, lo cual permite formar un total de ocho "tripletes":
+ + +, + + -, + - +, + - -, - + +, - + -, - - +, - - -
La transcripción propuesta consiste en asignar, entre estas secuencias, un 1 a las que están formadas por tres signos iguales (+ + + y - - -) y, para las restantes, un 3 a las que son simétricas o "capicúa" (+ - + y - + -) y un 2 a las que no lo son (+ + -, + - -, - + + y - - +). Resumiendo, tenemos la siguiente "tabla de asignaciones":
Otra diferencia con el ADN es que aquí los tripletes se superponen: por ejemplo, la secuencia + + - + se transcribe como 23, pues consiste en la concatenación de dos tripletes: + + - y + - +.
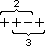
Por medio de este sencillo mecanismo el lector puede intentar "codificar" cualquier secuencia formada por signos + y -; por ejemplo, allí va la transcripción de algunas de ellas:
| + + + + |
-> |
1 1 |
| + - - + - |
-> |
2 2 3 |
| + + - + + + |
-> |
2 3 2 1 |
| - - - + + - + - |
-> |
1 2 2 2 3 3 |
| + + + - - + - + |
-> |
1 2 2 2 3 3 |
| |
... |
|
Los últimos dos casos llaman nuestra atención sobre un punto: dos secuencias diferentes pueden dar lugar a una misma transcripción. Esto obedece a un hecho muy elemental que no nos interesará aquí, aunque vale la pena señalarlo a fines de entender que la idea de "codificar" no era del todo correcta.
Una vez aprendido el mecanismo, un minucioso escriba podría ocuparse de construir, una por una, las secuencias bien formadas en el sistema {1-3}. Aunque la lista es interminable, ya desde el comienzo la tarea (un tanto tediosa) daría lugar a una observación: en este nuevo sistema no toda oración es bien formada. Eso nos pone ante el problema, nada trivial, de comprender su sintaxis.
A modo de entrenamiento, podemos efectuar la transcripción de todas las secuencias formadas por cuatro elementos del sistema {+,-}:
| + + + + |
-> |
1 1 |
|
- + + + |
-> |
2 1 |
| + + + - |
-> |
1 2 |
|
- + + - |
-> |
2 2 |
| + + - + |
-> |
2 3 |
|
- + - + |
-> |
3 3 |
| + + - - |
-> |
2 2 |
|
- + - - |
-> |
3 2 |
| + - + + |
-> |
3 2 |
|
- - + + |
-> |
2 2 |
| + - + - |
-> |
3 3 |
|
- - + - |
-> |
2 3 |
| + - - + |
-> |
2 2 |
|
- - - + |
-> |
1 2 |
| + - - - |
-> |
2 1 |
|
- - - - |
-> |
1 1 |
Esto nos brinda la lista completa de secuencias bien formadas de dos elementos en el sistema {1-3}: 11, 12, 21, 22, 23, 32, 33. Esto da un total de 6 secuencias entre las 8 posibles: en la lista faltan las secuencias 13 y 31, que no son bien formadas. La pregunta es: ¿hay forma de saber esto de antemano? Esto puede plantearse como un problema general: dada una combinación cualquiera en el sistema {1-3}, ¿existe algún procedimiento de decisión que permita saber si es bien formada? Tomemos una secuencia, por ejemplo:
11111122112333332222222222222211111111
¿Es bien formada?
Por cierto, podríamos tomar una moneda y arrojarla al aire cuarenta veces, aunque todos estarán de acuerdo en que sería una extraordinaria suerte si después de transcribirla obtenemos justo la secuencia deseada. También cabe la posibilidad de pedir a nuestro escriba que, como antes, nos brinde la lista exhaustiva (con sus respectivas transcripciones) de todas las secuencias posibles en el sistema {+, -}, que tengan una longitud de… ¡cuarenta símbolos! De esta forma, el test se reduce a observar si la oración que buscamos aparece en ella: como método, debemos decir que es infalible, aunque la perspectiva de examinar más de un billón[3] de palabras puede resultar algo desalentadora. El lector está invitado, como el último pretendiente del cuento, a mirar el problema de otra manera. Podemos anticipar que, en este caso, la mano de la princesa no es tan difícil de alcanzar.
Lo que no se puede decir, mejor callar
El título de esta sección es una frase muy conocida: se encuentra en la introducción al célebre Tractatus de Wittgenstein[4]. Se trata apenas del corolario -cuanto menos, honesto- de un hecho que casi un siglo más tarde podemos decir que no nos sorprende: hay cosas que el lenguaje no puede decir. Esta sentencia puede ser llevada incluso a un terreno bien concreto: por ejemplo, es fácil ver que ni siquiera la formidable combinatoria de caracteres fabulada por Borges (y mucho antes, por los cabalistas) en La biblioteca de Babel[5] alcanzaría para dar un nombre a cada uno de los números reales.[6]
Pero en vez de intentar decir algo acerca de lo que no es decible, podemos ver algo más inmediato, ligado a alguna versión lógica del "disparate". Al respecto, cabe recordar una poética tesis postulada en Adán Buenosayres, el libro de Marechal,[7] según la cual "el disparate no es de este mundo". Esto se ilustra con el siguiente ejemplo, al que unas breves líneas de riguroso análisis bastan para desmenuzar:
Cuando yo digo, verbigracia: El chaleco laxante de la melancolía lanzó una carcajada verdemar frente al ombligo lujosamente decorado, hay en mi frase, a pesar de todo, una lógica invencible.
En todo caso, hay un hecho que parece inobjetable: el lenguaje natural presenta una gran riqueza y cuenta con una variedad de recursos que permiten asociaciones semánticas de toda índole, por medio de metáforas y otros desplazamientos. De esta forma, no es difícil conectar una idea o una imagen con otra cualquiera. Nuestro objetivo es mucho más limitado y alcanza únicamente el campo de la sintaxis: vamos a ver que, en ciertos sistemas, determinadas secuencias de signos pueden considerarse, de algún modo, "disparatadas". A grandes rasgos, una combinación de signos que se sigue de las reglas puede ser denominada "teorema"; hemos mostrado algunos de ellos en el sistema {1 - 3}:
11, 223, 2321, 122233
Como anticipamos, en este sistema hay muchas palabras que no son bien formadas y desde el punto de vista de las reglas podrían considerarse "disparatadas": sin ir muy lejos, la lista completa de palabras de longitud 2 nos ha permitido ver que 13 y 31 se encuentran en tal condición.
Esta somera descripción no es suficiente para creernos en presencia grandes hallazgos, aunque al inspeccionar un buen número de palabras de mayor longitud quizás un investigador avispado sea capaz de observar una pequeña particularidad: nunca aparecen juntos un 1 y un 3. Esto es obvio en las palabras de longitud 2 y también se verifica en 223, 2321 y 122233. ¿Será siempre así? Un análisis más exhaustivo sigue confirmando este hecho; por ejemplo, podríamos volver a pensar en el "minucioso escriba" de la sección anterior para establecer la lista completa (por orden "alfabético") de todas las secuencias bien formadas pero ahora de tres números:
111, 112, 122, 123, 211, 212, 221, 222, 223, 232, 233, 321, 323, 333
Nuevamente, ni rastros de un 1 junto a un 3, lo que permite elevar a nuestra observación, prácticamente casual, al rango de conjetura:
Ninguna secuencia que contenga un 1 junto a un 3 es bien formada.
Una conjetura es un enunciado que se presume verdadero, pero que aún no ha podido probarse. Se trata de algo más que de una sospecha; en ocasiones, la presunta verdad se apoya en la comprobación de un gran número de casos particulares o, quizás, en alguna argumentación lógica que hace suponer que el enunciado es cierto. A veces la suposición falla y se prueba que una conjetura era falsa; en cambio, si alguien logra demostrar su verdad entonces el enunciado pierde el carácter provisorio de "conjetura" para transformarse, lisa y llanamente, en un teorema. En nuestro ejemplo, el proceso se ve coronado por el éxito: como puede comprobarse a partir de las reglas, ninguna secuencia del sistema {1 - 3} contiene un 1 junto a un 3. Si tenemos un 1, proveniente por ejemplo de la secuencia +++, entonces ningún signo que agreguemos a continuación produce un 3:
+ + + + -> 11
+ + + - -> 12
La demostración se completa analizando los restantes casos posibles; en otras palabras, cualquier secuencia en donde aparezcan juntos un 1 y un 3 es "disparatada".
1, 2, 3,... ¡A interpretar!
Hemos hablado al comienzo de la princesa y sus diversos pretendientes; podemos plantear ahora una situación contraria, en la que dos princesas son cortejadas por un mismo joven. Los respectivos palacios se encuentran separados por un río; cuando se encuentra de visita en la región el joven elige día tras día, según le dicten sus ánimos, a cuál de ellas visitar. En ocasiones se queda muchos días y ve muchas veces a cada una: pasa la noche en algún hotelito cercano al último palacio visitado y al día siguiente decide si vuelve a ver a la misma princesa o si atraviesa el río para reunirse con la otra. Sin embargo, quiso el destino que la barca que efectúa el trayecto sea conducida por una bonita muchacha; por tal razón, el apasionado joven cruza el río una o más veces por el sólo placer de navegar junto a ella. Más aun: puede ocurrir que en alguno de sus viajes se dirija directo al embarcadero, antes de visitar a cualquiera de las princesas. Lo que se dice un corazón inquieto.
Sin embargo, en su favor podemos decir que se trata de una persona muy ordenada -en especial en cuestiones amorosas- y siempre lleva en su cuaderno un cuidadoso registro de sus encuentros, tanto con las princesas (por discreción, las llamaremos A y C) como con la barquera (B). Por ejemplo, esta es una de sus páginas:
Primer día: visito a la princesa A.
Segundo día: visito a la princesa A.
Tercer día: cruzo el río y visito a la princesa C.
Cuarto día: cruzo el río y visito a la princesa A.
Quinto día: cruzo el río y vuelvo a cruzarlo; hoy B está tan linda que lo cruzo otras dos veces antes de volver finalmente al palacio de A.
Dejando de lado los detalles, las notas pueden resumirse así:
AABCBABBBBA
A la larga, estas "memorias" se tornan un tanto tediosas... Pero hay algo que es claro: luego de ver a una de las princesas nuestro galán debe cruzar un número impar de veces el río para ver a la otra y un número par (lo que incluye la perspectiva de no cruzarlo) si quiere repetir su visita.
A esta altura, no estaría mal preguntarnos a qué viene todo este asunto de princesas y barqueras bonitas. La respuesta es muy simple; como insinúa el título de la sección, nuestra historia de amores múltiples brinda una interpretación de aquel sistema cuya sintaxis no hemos terminado de describir: el sistema {1 - 3}. En efecto, basta con establecer el siguiente correlato:
A -> 1
B -> 2
C -> 3
Es fácil verificar que la manera de concatenar las secuencias de signos + y - para generar las secuencias numéricas se encuentra bien "correspondida" en el hecho de que el joven puede visitar a una misma princesa tantas veces seguidas como le vengan en gana, pero no puede ver a una después de la otra en forma sucesiva sin atravesar el río. Por cierto, falta verificar los detalles, tarea que queda a cargo del lector. Pero una vez que nos convencemos de que la interpretación es adecuada, resulta sencillo encontrar, como habíamos dicho, un "procedimiento de decisión" para las secuencias del sistema. Por ejemplo, había quedado pendiente la cuestión de saber si la siguiente secuencia es bien formada:
11111122112333332222222222222211111111
¿Qué podemos decir ahora? En el "universo" fijado para nuestra interpretación, la última tira de 2 que aparece antes de la secuencia 11111111 corresponde a sucesivos paseos en bote: en total, catorce. En principio, eso parecería indicar que la barquera está hoy especialmente irresistible, cosa que se ajusta perfectamente a los supuestos de nuestra historia. Pero hay algo que no encaja: antes de esta "tira" aparece un 3 y a continuación de ella un 1. Eso significaría que los catorce paseos tuvieron lugar entre una visita a la segunda princesa y una visita a la primera. Según dijimos, eso no puede ser, lo que nos permite dar una respuesta precisa al asunto: la secuencia anterior no es bien formada.
Esto no es más que un ejemplo elemental, pero suficiente para apreciar los beneficios que puede llegar a tener una buena interpretación.
Notas
- Pablo Amster: La matemática como una de las bellas artes, Siglo Veintiuno Editores, Buenos Aires, 2004.
- Jacques Lacan: "El seminario sobre La carta robada", en Escritos 1, Siglo Veintiuno Editores, Buenos Aires, 2002.
- El número exacto es 240 = 1099511627776.
- Ludwig Wittgenstein: Tractatus Logicus-Philosophicus, Editorial Altaya, Barcelona, 1994.
- Jorge Luis Borges: "Ficciones (1936), El jardín de los senderos que se bifurcan (1941), La biblioteca de Babel", en Obras Completas (1923-1972), Emecé Editores, Buenos Aires, 1974, pp. 465-471.
- Cabe aclarar que en el cuento de Borges los libros están limitados en su extensión, con lo cual la afirmación se vuelve trivial pues los números son infinitos. Pero el hecho matemático interesante que señalamos consiste en que ni siquiera las infinitas palabras que podrían formarse combinando los caracteres de un alfabeto finito alcanzarían para nombrar a los reales, que conforman un infinito mayor. Ver Pablo Amster: Apuntes matemáticos para leer a Lacan (en prensa).
- Leopoldo Marechal: Adán Buenosayres, Editorial Sudamericana, Buenos Aires, 1973.
Autor de los cursos a distancia:
|