Textos de acceso libre
Qué modelo hay que tomar para seguir.
Dr. Pablo Amster.
Buenos Aires 31 de marzo de 2020.
En rigor toda la epidemiología, relacionada como está con la variación de una enfermedad en el tiempo y de un lugar a otro, debe ser considerada matemáticamente, sin importar cuántas variables implicadas haya, si es que se la quiere considerar de manera científica. Sir Ronald Ross.
Se puede leer así. También puede leerse, puesto que está en letras mayúsculas, puede leerse: R - S - I, lo que quizá ha sugerido, a los que están advertidos: lo Real, lo Simbólico y lo Imaginario. J. Lacan, RSI.
Estos tiempos de pandemia son, también, tiempos de pandemonium: como nunca antes, se multiplican las voces (virtuales, en su mayoría) que opinan y desopinan sobre los distintos cursos de acción que deberían seguir las personas, las familias o los gobiernos. En particular, las políticas de aislamiento que se han adoptado en la mayoría de los países se fundamentan, como se dice aquí y allá, en la importancia de achatar la curva. Ahora bien, ante tales afirmaciones, más de uno puede sentirse “desorientao”, sin saber qué curva hay que achatar. Es fácil entender en qué consiste el “distanciamiento social”, especialmente cuando se lo vive en carne propia (vale decir, lejos de otras carnes). Es fácil, también, entender que si se reducen los contactos se reducen también los contagios; por eso, la mayoría acepta la idea del confinamiento como una forma efectiva de prevenir el avance del virus.
Lo que quizás muchos ignoran es que estas conclusiones no se apoyan en observaciones más o menos triviales sino en modelos matemáticos que, con mayor o menor éxito, han permitido explicar y predecir distintos fenómenos en epidemiología.
El objetivo de estas líneas consiste en exponer brevemente los fundamentos principales del más célebre de dichos modelos, el llamado modelo SIR, cuyos orígenes se encuentran en los estudios sobre la malaria llevados a cabo por Ronald Ross, premio Nobel y nombrado justamente Sir en 1911 por la corona británica.
Ante todo, ¿qué es un modelo? Aquí el lector de Lacan podrá recordar aquello de “extrapolar en lo Real”, que lo lleva a ubicar el modelo del lado de lo Imaginario y, a nosotros, muy cerca del punto de partida. Por eso, es mejor dejar de “lacanear” por un rato y observar simplemente que la noción intuitiva de modelo se refiere a una formalización, es decir, la representación de algún fenómeno por medio del lenguaje matemático. Por supuesto, la asignación de términos, relaciones y operaciones no es caprichosa, sino que debe seguir ciertos principios básicos. A grandes rasgos, se espera que funcione como una buena explicación del fenómeno que pretendemos describir y tenga alguna capacidad predictiva: así, en un modelo como el de Newton, vemos que las leyes de la física cobran el aspecto de fórmulas matemáticas tales como F = ma, que permiten, entre otras cosas, calcular la trayectoria de un cuerpo si conocemos las fuerzas que actúan sobre él. Hay modelos para todo, desde la física o la biología hasta los comportamientos sociales, las finanzas y las catástrofes (aunque, en el momento actual, no es fácil distinguir entre las dos últimas).
Pero no se trata de hacer un desfile de modelos sino de explicar, como dijimos, las bases de aquel que quizás sea el más simple de los que se emplean para describir epidemias. Claro que, en este caso, las letras mayúsculas S - I - R no corresponden a los registros lacanianos sino a tres grupos en los que se divide una población, Susceptibles, Infectados y Recuperados, regidos por la siguiente dinámica:
S → I → R
Esto significa que en cada instante algunos individuos del grupo S se contagian y pasan al grupo I mientras que, a su vez, algunos individuos del grupo I se recuperan, pasan al grupo R y allí permanecen, pues ya no pueden volver a contraer la enfermedad. Por simplicidad, se asume que la población total permanece constante, es decir, que no hay nacimientos o muertes. Esto puede parecer un desatino cuando se trata justamente de una enfermedad mortal, aunque se arregla incluyendo en el grupo de recuperados también a los que mueren. Eso sí, antes de que todos pongan el grito en el cielo (por así decirlo), hay quienes optan por reemplazar el término “recuperados” por el de removidos: una manera algo más elegante de decir que del tercer grupo no se vuelve.
Para cuantificar esta dinámica, se toman en cuenta dos parámetros fundamentales que especifican la proporción de individuos que pasan de un grupo a otro: una tasa de transmisión, habitualmente denotada mediante la letra griega β (beta) y una tasa de recuperación, llamada γ (gamma). El valor de β se establece a partir del promedio del número relativo de individuos con las que una persona se contacta, multiplicado por la probabilidad de que un contacto se transforme efectivamente en contagio. El valor de γ suele ser el inverso del período medio de “recuperación”, vale decir, del tiempo que tarda un infectado en dejar de serlo.
Pero para llegar a las ecuaciones del modelo SIR falta introducir todavía un concepto clave, el de derivada que, a grandes rasgos, mide la variación instantánea de una determinada cantidad. Por ejemplo, la velocidad nos dice cómo varía el espacio recorrido respecto del tiempo transcurrido; la aceleración no es otra cosa que la variación de la velocidad. Sin embargo, la idea de “instantánea” es un poco más esquiva y costó algún esfuerzo definirla con rigor matemático: ¿cómo calcular la variación que se produce en un instante, en el que el tiempo justamente no transcurre?
Lo que se puede, por ejemplo, es medir el espacio que se recorre en un intervalo de tiempo y calcular entonces la velocidad media en dicho intervalo. Pero para establecer la velocidad instantánea deberíamos suponer que el intervalo temporal se hace más y más pequeño y, en consecuencia, también es cada vez más pequeña la distancia recorrida. Esto da origen al cálculo infinitesimal, que motivó incisivas críticas en los tiempos de Newton y Leibniz. En particular la del obispo Berkeley, para quien que los misterios de la fe no eran más misteriosos que los principios de la ciencia newtoniana y describió los infinitésimos de una manera muy sugestiva: fantasmas de cantidades desaparecidas. Pero más allá de las notables cualidades retóricas del obispo, el hecho es que sus observaciones sobre el trabajo de Newton no eran nada tontas y forzaron a los matemáticos de los siglos posteriores a establecer con mucho mayor cuidado los fundamentos del análisis. La noción que permite hacer todo como corresponde (o, preferiría tal vez Berkeley, como Dios manda) es la de límite que, lejos de ser un misterio, responde a una definición rigurosa.
Aceptemos entonces sin más reparos esta idea intuitiva de la derivada como tasa instantánea de cambio: una cantidad que varía con el tiempo se expresa como una función C(t); su derivada en cada instante t se escribe C’(t).
En el caso del modelo SIR las funciones que intervienen son tres, por eso diremos que se trata de un sistema. Y el tipo de ecuaciones que lo componen son ecuaciones diferenciales, en las que las que existe algún tipo de relación entre las funciones y sus derivadas. Para deducir tales ecuaciones, observemos que en cada instante una cierta cantidad de individuos se contagia, es decir, pasa del primer grupo al segundo. ¿A qué velocidad lo hace? En principio, si multiplicamos β por la cantidad I(t) de infectados, eso nos da la proporción de nuevos contagios que se producen; a su vez, este valor hay que multiplicarlo por la cantidad S de susceptibles, que son los únicos que pueden contagiarse. De esta forma, la cantidad de susceptibles disminuye en el tiempo de acuerdo con la siguiente fórmula:
S’(t) = -βI(t)S(t)
De la misma forma, una cierta cantidad del grupo de infectados pasa en cada instante al tercer grupo; la velocidad con que esto ocurre se obtiene multiplicando el parámetro γ por I(t). Luego, la cantidad de recuperados cumple la ecuación
R’(t) = γI(t)
Finalmente, la dinámica del grupo de infectados se explica de manera inmediata a partir de lo anterior: en cada instante se agregan los que provienen del segundo grupo y se restan los que pasan el tercero. En otras palabras:
I’(t) = βI(t)S(t) - γI(t).
He aquí la famosa curva. Uno podrá objetar que hemos visto muchas fórmulas pero todavía ningún dibujo, aunque cabe sospechar que lo que vamos a graficar son justamente las soluciones de estas ecuaciones diferenciales. Dichos gráficos van a depender de los distintos valores iniciales que asignemos a la cantidad de susceptibles e infectados (siempre se asume que el valor inicial R(0) es 0). Es oportuno señalar que las funciones S(t), I(t), R(t) no se calculan de manera explícita, pero es posible verificar diversas propiedades que determinan su comportamiento.
En primer lugar, siempre se supone que la cantidad inicial de infectados es positiva, pues en caso de ser nula nadie se contagia y toda la población se mantiene fija, sanita y coleando, dentro del grupo S. Pero entonces es fácil demostrar que I(t) y S(t) se mantienen siempre positivos; en consecuencia, la derivada de S es negativa, y eso implica que la cantidad de susceptibles disminuye para todo valor de t. Del mismo modo, la derivada de R es positiva y luego la cantidad de individuos en el tercer grupo aumenta a medida que lo hace t.
Hasta ahora no hay mayores sorpresas, aunque la cuestión crucial viene dada por la ecuación para el número de infectados. De acuerdo con lo que dijimos, I(t) aumenta o disminuye según sea positivo o negativo el valor de su derivada, es decir, del término βI(t)S(t) - γI(t). Pero esto es igual a (βS(t) - γ)I(t) y, dado que I(t) es positivo, alcanza con observar el signo de βS(t) - γ. Ahora, recordemos que S(t) es decreciente, de modo que hay dos posibilidades:
- βS(0) - γ < 0 y en consecuencia βS(t) - γ < 0 para todo t. En tal caso, el número de infectados siempre disminuye. ¡Genial! Eso quiere decir que la presencia inicial de algunos infectados no fue más que un susto… aunque, lamentablemente, no es lo que ocurre en nuestra situación actual.
- βS(0) - γ > 0. En ese caso, la cantidad de infectados va en aumento (¡epidemia!) hasta que, para cierto t* vale βS(t*) = γ. A partir de allí, el número de infectados decrece.
Llegado este punto, una pregunta pertinente es: ¿cómo estamos tan seguros, en el segundo caso, de que existe el dichoso valor t*? ¿No podría ocurrir que el número de infectados sea siempre creciente?
La respuesta es que, inexorablemente, en algún momento el número de infectados comienza a bajar. Esto es un ejercicio elemental para cualquiera que haya hecho un curso de análisis matemático: si I(t) fuera siempre creciente, llegaría un tiempo en el que el valor de R(t) superaría la población total, lo que es absurdo. Es fácil ver, en rigor, que I(t) siempre tiende a 0 pero S(t) no: en otras palabras, a la larga la enfermedad siempre se extingue y esto ocurre antes de que todos hayan sido contagiados. En el fondo, se trata de buenas noticias.
Tenemos entonces una función I(t) que comienza creciendo y luego, a partir del valor t*, empieza a bajar. El siguiente gráfico muestra, de manera esquemática, el comportamiento de las tres funciones: I (azul), S (amarillo), R (rojo).
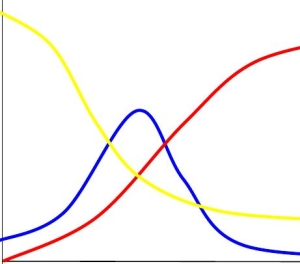
Pero volvamos a la ecuación de I(t), que puede escribirse así:
I’(t) = (βS(t) - γ)I(t)
Como dijimos, lo que determina el crecimiento o decrecimiento de I es el hecho de que el valor βS(t) esté por encima o por debajo de γ. Esto ocurre al comienzo, cuando la población de susceptibles es todavía grande; más aún, cuando el número de infectados todavía es muy pequeño, el valor de S varía muy poco en términos relativos. Por ejemplo, supongamos que en una población de 10 millones de personas aparecen 1, 5, 100 infectados: por el momento, la cantidad de susceptibles sigue siendo esencialmente igual a 10 millones. Eso explica por qué, al comienzo, la curva de infectados tiene el (¡temible!) comportamiento exponencial: la ecuación “se parece” a otra de la forma I’(t) = CI(t) donde C es constante, cuyas soluciones son precisamente funciones exponenciales.
Esto es algo que se escucha a menudo en los medios, aunque en muchos casos no queda claro de qué se trata. La manera más sencilla de explicar este comportamiento exponencial consiste en decir que los valores de la función, a intervalos regulares, siguen una progresión geométrica. Lo que más se ha difundido en estos días es el llamado tiempo de duplicación, vale decir, la cantidad de días requeridos para que I(t) duplique su valor. Por ejemplo, si el tiempo de duplicación fuera de 3 días, entonces a partir de 5 infectados el día 0 tendremos 10 infectados el día 3, 20 infectados el día 6, 40 el día 9, etc. Es claro que este ritmo no puede mantenerse por mucho tiempo: al cabo de 60 días, por ejemplo, la población se habría duplicado 20 veces y la cantidad de infectados sería 5.220 = 5242880. Y si esperamos 30 días más prácticamente toda la población del planeta estaría infectada. El comportamiento exponencial se observa al comienzo pero, a medida que la cantidad de susceptibles baja, la curva de infectados detiene su crecimiento desenfrenado para -poco a poco- revertirse y empezar a decrecer.
Pero volviendo al comienzo: ¿qué es eso de aplanar la curva? No es difícil entender que la idea clave es lograr que la curva de infectados no crezca de manera tal que los sistemas sanitarios se vean colapsados. Como el crecimiento en la cantidad de infectados depende de βS(t) - γ, lo deseable es que esta cantidad sea suficientemente baja mientras todavía no se infectó tanta gente, es decir, mientras S(t) sigue siendo grande. Como el valor de γ no depende de lo que hagamos, la única forma de lograr el cometido consiste en reducir el valor de β. Claro que esta no es la instrucción literal que van a dar los organismos gubernamentales a la ciudadanía (¡Señoras y señores, bajen β!), sino más bien una versión equivalente: quédense en casa. Si se reducen al máximo los contactos, el valor de β disminuye y, en definitiva, el pico en la curva de infectados se hace menos violento.
El modelo SIR, como dijimos, es el más simple y tiene múltiples variantes. En particular, dadas las características de este virus se emplea una versión ligeramente distinta, con una ecuación más que corresponde a los expuestos: aquellos que ya tienen la enfermedad pero aún no presentan síntomas y, por consiguiente, no forman parte del grupo de infectados. El nombre del modelo resultante, SEIR no tiene ya connotaciones psicoanalíticas, aunque el juego de reordenar sus letras permite obtener uno de los heterónimos del poeta portugués Fernando Pessoa. Se trata de otro médico, Ricardo Reis, cuya obra expresaba la doctrina epicúrea, basada en el buen vivir y la serenidad. Bien entendida, ¿no es acaso la mejor forma de atravesar este momento?
[...] He aquí el día,
he aquí la hora, he aquí el momento, esto
es lo que somos, y esto es todo.
Fluye perenne la hora interminable
que nos declara insignificantes. En el mismo sorbo
en que vivimos, moriremos. Toma
el día, porque es él.
Ricardo Reis, Odas
Autor de los cursos a distancia:
|