Textos de acceso libre
PSICO-ANALYSIS SITUS
Un artículo de situación. Breve introducción a la topología.
Dr. Pablo Amster *
Breve introducción a la topología
1. Sensatez y presentimientos
Hace cuarenta años -más precisamente,
el 7 de marzo de 1962- Lacan formulaba durante su clase del seminario La
Identificación un misterioso anuncio:
Pues es del toro que voy a hablarles hoy.
Abro deliberadamente, como ustedes lo ven, a partir de hoy, la era
de los presentimientos.
Cabe imaginar que tan deliberada apertura debió suscitar entre
la audiencia cierta inquietud, que dudosamente iba a mitigarse por el
posterior aviso:
Intentemos ahora aclarar lo que voy a decirles.
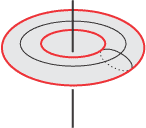
Cualquier estudiante sabe lo que es un toro, al que fructíferos
siglos de geometría han definido como una
superficie de revolución engendrada
por una circunferencia que gira en torno a un eje situado en su mismo
plano y exterior a la misma.
También podemos ubicarnos en aquel punto del
siglo XVII, en el que otro notable francés se dio el gusto de proclamar
sus propios anuncios:
10 de noviembre de 1619, cuando lleno de
entusiasmo, descubrí los fundamentos de una ciencia admirable.
Se trata de Descartes, quien sin duda abrió
una era al presentar su formidable conjunción entre geometría
y álgebra, descripta en estos términos por Edgar Quinet:
Cuando vi a esta ecuación funcionar
y resolverse sola, por así decir, entre mis manos, y explotar
en una infinidad de verdades, todas igualmente indudables, creí
estar en posesión del talismán que me abriría
la puerta de todos los misterios.
Parece justo, entonces, que brindemos el talismán capaz de abrirnos
la puerta de los misterios correspondientes a la figura que nos concierne
aquí, resumido en una expresión de lo más concisa:
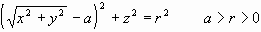
Sin embargo, no parece ser el camino cartesiano el
más apropiado para que algo se nos aclare: ¿cómo pueden
esas letras ser capaces de manifestar la esencia del toro?
Más aun, ¿cuál es dicha esencia?
La respuesta a esta pregunta constituye el comienzo de lo que Lacan va
a decirnos, que más tarde iba a expresar mediante el juego de palabras trou matisme: la esencia de un toro es tener un agujero.
Cabe indicar que esta observación, casi trivial, deja de lado importantes
aspectos métricos del toro para centrarse en su carácter
puramente cualitativo: en otras palabras, estamos hablando de una propiedad
relativa a aquella materia que Gauss describe en 1833 como
la geometría de situación, que Leibniz
ha presentido...
Vemos así que también la Matemática avanza en base
a presentimientos, en muchos casos producto de las mentes más sensatas.
El presentimiento leibniziano llevó durante algún tiempo
el nombre -propuesto por el autor- de Analysis Situs, hasta que
en 1847 el matemático Listing acuñó la que sería
su denominación definitiva: topología.
2. Geometría cauchesca
La topología es considerada actualmente una
de las principales ramas de la Matemática, aunque su desarrollo es
relativamente reciente, como se evidencia en la continuación de la
anterior cita gaussiana:
...sobre la cual ha estado reservado a dos
geómetras solamente, Euler y Vandermonde, echar una débil
mirada, sabemos y poseemos, después de siglo y medio, poco
más que nada.
Más allá de la anticipación del
nada cándido Leibniz, los historiadores suelen conceder un
rol inaugural al gran matemático Euler, cuando desde la corte de
Catalina (también Grande) en San Petersburgo resolvió
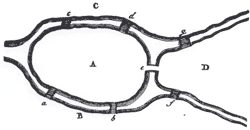
el famoso problema de los puentes de Königsberg:
El río Pregel atraviesa la ciudad
de Königsberg formando dos islas que se unen entre sí
y con tierra firme mediante siete puentes. ¿Es posible trazar
un recorrido que pase por todos los puentes cruzándolos una
sola vez?
Acaso para extrañar un poco menos a su Suiza
natal, Euler se convenció de que la distancia no importa,
al menos a la hora de resolver esta clase de problemas. En efecto, el acertijo
se resuelve mediante un sencillo modelo llamado grafo, en
el cual las líneas o aristas representan los puentes, y los
puntos (vértices) las regiones conectadas por ellos.
Es fácil comprobar entonces que el recorrido
propuesto es imposible, por una razón que casi parece lacaniana:
la paridad. Un vértice se dice par o impar de
acuerdo con la cantidad de aristas que lo tienen como extremo, y resulta
claro que un vértice que sea odd (impar) sólo puede
ser punto inicial o punto final de un recorrido. Bajo esta óptica,
Euler no hizo más que señalar lo que está a la vista:
dado que todos los vértices son impares, cualquier itinerario que
se trace fuerza a la repetición de al menos un puente. Este
sencillo proceder nos muestra el aspecto más intimo de un
problema que, una vez despojado de aditamentos, se reduce a puras consideraciones
de orden combinatorio. Nada de distancias o ángulos; el razonamiento,
sutil pero poderoso, permitió a su artífice brindar la respuesta
apropiada y -de paso- dar comienzo a una disciplina: al fin y al cabo, ¿qué
mejor que una corte para fundar la topología?
Una antigua frase asegura que la geometría es el arte de razonar
sobre figuras mal hechas. Al respecto, Poincaré se pregunta: ¿Pero
qué es una figura mal hecha? En la geometría clásica
dos figuras son equivalentes cuando se las puede superponer mediante rotaciones y traslaciones; en ese caso podemos aceptar que éste

es un círculo mal hecho. En cambio,
no lo es para la geometría proyectiva, que prescinde de algunos
aspectos métricos para apoyarse sobre la noción de perspectiva.
Un círculo es equivalente a una elipse porque una figura es una perspectiva
de la otra. Pero aun así estaremos de acuerdo en que esta otra

es una elipse muy mal hecha, pues no parece
haber punto de vista capaz de limar las asperezas de sus ángulos.
Como dijimos, la topología suprime las cantidades y sólo
se fija en cualidades; en ella, dos figuras son equivalentes siempre
que se pueda pasar de una a la otra por medio de una deformación
continua. Lo que se preserva entonces son las características
realmente esenciales de las figuras, llamadas invariantes topológicos.
Este aspecto tan "flexible" de la topología justifica ese
nombre coloquial con que también se la conoce: geometría
del caucho.
El geómetra clásico tiene como herramientas la regla y el compás; sin embargo, Poincaré encuentra el verdadero
papel de la intuición geométrica precisamente en aquella
ciencia que se desentiende toda medida:
...es para favorecer tal intuición
que el geómetra tiene la necesidad de dibujar figuras o, por
lo menos, representárselas mentalmente. Ahora bien, si desprecia
las propiedades métricas o proyectivas de estas figuras, si
sólo se atiene a sus propiedades puramente cualitativas, solamente
entonces la intuición geométrica interviene verdaderamente.
Como se advierte (o presiente) desde el subtítulo,
este artículo está destinado a situar a esta curiosa geometría [1], en particular en lo que hace
a un tema de permanente actualidad: la formación del analista.
Después de todo no fue otro sino Lacan quien, pocos años antes
de introducir al toro, ligara en uno de sus escritos a ambos términos, situación y formación [2].
Referencia bibliográfica:
- Para una introducción a la
topología, ver P.Amster, La matemática en la enseñanza
de Lacan.
- J. Lacan, Situación del psicoanálisis
y formación del psicoanalista en 1956.
Autor de los cursos a distancia
|